KARE KESİTLİ BİR HAVA KANALINDA AKİS İÇİN DENEYSEL BİR YAKIŞIM Kare Kesitli Bir Hava Kanalında Akis İçin Deneysel Bir Yaklaşım

05 Ocak 2000 Dergi: Ocak-2000

1. Giriş
Hem şekil hem de imalat kolaylığı ve gerilmelere dayanıklılık bakımından avantaj sağladığı için çeşitli mühendislik uygulamalarında genellikle dairesel kesitli borular kullanılır. Ancak gelişen teknoloji ile birlikte farklı kesitli boru kullanımı gittikçe artmaktadır. Son yıllarda, ısıtma, havalandırma, iklimlendirme ve soğutma sistemlerinde, bacaların, gaz ve havalandırma kanallarının dizaynında kare ya da dikdörtgen kesitli boru kullanımı yaygınlaşmıştır. Çeşitli hava kanalları sistem tasarımı yapılırken kullanılan malzemenin cidar pürüzlülüğü; gürültü seviyesi, kanallardaki ısı kazançları ve kayıpları ve sistemin işletme masrafları açılarından oldukça önem taşımaktadır 11], |2|.
Bu çalışmada, kare kesitli bir kanal içerisinde türbülanslı hava akışı halinde cidar pürüzlülük katsayısı ve yüzey pürüzlülük sınıfını tespit etmek amacıyla basit bir deneysel metod kullanılmış ve literatürde geliştirilen çeşitli ampirik bağıntılara ve diyagramlara hangi ölçüde yaklaşılabilece-ği araştırılmıştır

2. Türbülanslı Akış Teorisi
Türbülanslı akışlar ile ilgili araştırmaların tarihi, laminar akışlar gibi çok eski olmasına rağmen akışın karakteristikleri tam olarak anlaşılmaktan uzaktır. Son yıllarda önemli ilerlemeler gösteren bilgisayar karakteristikleri tam olarak anlaşılmaktan uzaktır. Son yıllarda önemli ilerlemeler gösteren bilgisayar teknolojine bağlı olarak sayısal çözüm yöntemlerinin gelişmesi, türbülanslı akışlar hakkında daha ayrıntılı bilgiler elde edilebilmesini mümkün kılmıştır, Laminar ve türbülanslı akışlarla ilgili çalışmalar, bilindiği gibi ilk defa Reynolds, I883 tarafından gerçekleştirilmiştir. Daha sonraki yıllarda Blasius, 1908; Prandtl, 1921; lakop ve Erk, 1924; Kirstan, 1927, Heimann, 1930; Nikuradse ve diğ. 1932; Stanton ve diğ. I959 gibi araştırmacılar deneysel ve analitik birçok çalışma gerçekleştirmiştir |3|, |4],|5],|6|.
Bu çalışmalarda, özellikle değişik ge-ometrili borulardan akışkan geçirilerek günümüzde hâlâ yaygın olarak kullanılan diyagramlar, ampirik ve yarı ampirik bağıntılar sunularak laminar ve türbülanslı akışkanların genel karakteri hakkında fikir verilmektedir |6|,

Sürekli rejim türbülanslı akış için, zaman ortalamalı iki boyutlu momen-

3. Deneysel Yöntem ve Hesaplamalar
3.1. Deney Düzeneği
Deneysel çalışmalarda kullanılan dü¬zeneğin prensip şeması Şekil İde gösterilmiştir. Test için kullanılan de¬ney borusu, l 75 m uzunlukta ve kesi¬ti 0 l x 0 l m' olan bir kanaldır. Kanal, türbülanslı akışlarda hidrodinamik tam gelişme için yeterli uzunluktadır Akışı sağlayan fanın devri bir varyak yardımıyla ayarlanmakta ve böylece farklı debilerde hava akımı elde edil¬miştir. Tam gelişmeyi sağlayan ana borunun (5-5) kesitinde, kanalın tam merkezine yerleştirilmiş bir pitot tüpü ve eğik manometre yardımı ile debi kontrol edilmiştir. Buraya bağlı eğik manometreden okunan Hk yükseklik¬leri üç ayrı debi için elde edilmiş ve Şekil 2'deki u-Hk kalibrasyon eğrisi çi¬zilmiştir. Defti kalibrasyon eğrisi kul¬lanılarak, varyakın herhangi bir duru¬mu veya Hk'nın belli değeri için dik kesit içindeki ortalama hız (u) saptan¬mıştır Ortalama hız (u)'nun belirlen¬mesi ile ilgili detayla? aşağıdaki su¬nulmuştur. Test bölgesinde (6-6' kesitinde) diğer bir eğik manometre ve y yönünde mikrometreli bir pitot tüpü kullanılarak, 5 mm aralıklarla eksen¬den cidara doğru basınç değerleri okunmuştur. Civa genleşmeli termo¬metre ile kanaldan akan havanın sı¬caklığı ölçülmüştür.
3.2 Ortalama Hızın Belirlenmesi
Debi birvaryakyardımı ile belli birde-ğere sabitleştirildikten sonra (Hk=sa-bit) boru çıkışında y yönünde mikro¬metre ve x yönünde bir ölçek kullanı¬larak pitot tüpü yardımı ile her nokta¬ya ait (toplam 25 nokta) ux eksenel hız değerleri ux=(2AP/ph)'J eşitliği kullanılarak hesaplanmıştır. Ölçümün yapıldığı kesit alanı (100x100 mm") her biri 4 cm1' alanlı ax kareciklerine bölünerek, ölçümler bu karelerin orta noktalarında yapılmıştır (Şekil 3). Ha¬vanın fiziksel özellikleri ortalama hava sıcaklığı esas alınarak seçilmiştir. Dik kesitteki ortalama hız ise aşağıdaki ifadeden hesaplanmıştır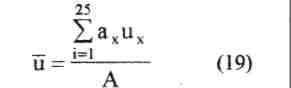

Bu   eşitlikte,   ax=4   cm2   ve   A=IOO crrr'dır
3.3. Boyutsuz Hız ve Boyutsuz Cidar Mesafesinin Belirlenmesi
Üç farklı Hk için test bölümünün 90 cm'lik aralığında (7-7') statik basınç yükseklikleri H ölçüldükten sonra; ba¬sınç kaybı (AP), kayma gerilmesi (xw) sürtünme hızı (u*) aşağıdaki eşitlik¬lerden hesaplanmıştır.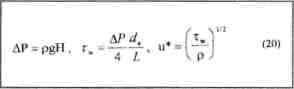

Üç farklı sabit debi için boyutsuz hız <P = u/u* ve boyutsuz cidar mesafesi I nr|=ln(yu*A>) değerleri hesaplanmış ve Şekil 4'deki evrensel hız diyagramı elde edilmiştir
4. Bulguların Değerlendirilmesi
Şekil 4'deki doğrusal ilişkiden fayda¬lanılarak, (16) eşitliğindeki D sabiti 5 olarak tespit edilir. Bu eğim değeri ve A=1/K eşitliğinde kullanılarak K sabiti hesaplanır. Örneğin <î> = u/u* = 30 se¬çildiğinde, lnr|= 6 3 ve K=0.25 olarak bulunur, K ve D sabiti, (17) eşitliğinde yerine konursa, P = 0.286 olarak he¬saplanır. Şekil 4'de görüleceği üzere, T) değeri 4 ila 7 arasında değişmekte¬dir. Bu değer, akışın büyük yaklaşıkla laminar sürtünme bölgesinde kaldığı¬nı göstermektedir. Bu yüzden deneylerin gerçekleştirildiği kanalın pürüz¬süz boru sınıfına girdiği söylenebilir. Şekil 5'de üç farklı debi için tam geliş¬me bölgesinde kanal kesitinde ölçü¬len eksenel hız profilleri gösterilmiş¬tir. Şekilden görüleceği üzere, elde edilen hız profillerinin türbülanslı akıştaki hız profillerine çok az sapma¬larla yaklaşmıştır. Bu da kullanılan deneysel metodun doğruluğunu gös¬terir mahiyettedir. Bu çalışmada elde edilen sonuçlar aşağıda özetlenmiştir:
a. Kullanılan deneysel yöntem ile
elde edilen sonuçlar literatürle
uyum halinde olduğu tespit
edilmiştir.
b. Mevcut çalışmadaki evrensel
diyagramı esas alındığında K=0.25,
D=5.0 ve (3=0.286 olarak
bulunmuştur. Nikuradse
tarafından yapılan deneylerde bu
katsayısılar sırasıyla 0,4, 5.5
ve 0,111 olarak tespit edilmiştir. Söz konusu farklar, deney setinin ve ölçüm aletlerinin hassasiyeti ve boru çıkışına yakın ölçme yapılması dolayısıyla akışın engellenmesi yüzündendir.
c. Deney yapılan kanalın tamamıyla
laminar sürtünme şartlarında akım
sağladığı gözlenmiştir. Bu yüzden
sanayide kullanılan sac
malzemelerini pürüzsüz kabul
etmek uygun olacaktır.
Semboller
A    : Borunun kesit alanı, eğim
ax   : Boru dik kesitindeki bölünmüş alan
C     : integral sabiti
de   : Eşdeğer hidrolik çap
D,(3 : Boru pürüzlülük katsayısı
H    : Eğik manometreden okunan yükseklikler
Hk : Kalibrasyon eğrisi eğik manometre değerleri
L    : Boru uzunluğu
u    : Bir noktadaki zaman içindeki ortalama hız
u     : Boru çıkışındaki kesitte hesaplanan ortalama hız
ux   : Çıkışta kesitte ax alanına ait
hızlar
u* : Sürtünme hızı
x,y : Koordinatlar
y0 : Cidara çok yakın mesafe
Y : Borunun yüksekliği
AP : Basınç kaybı
et : Eddy kinematik viskozitesi
A. : Sürtünme katsayısı
K : Evrensel sabit
P : Prandtl karışım yolu uzunluğu
u. : Dinamik viskozite
p : Yoğunluk
u.t : Eddy dinamik viskozitesi
TW : Cidar kayma gerilmesi
xt : Türbülanslı kayma gerilmesi

i]    : Laminar kayma gerilmesi
t)    : Kinematik viskozite
<t>    : Boyutsuz hız
r     ■ Borunun ekseninden cidara olan boyutsuz mesafe
Kaynaklar
i.    Genceli, OF., Ashrae Temel El Kitabi: Kanal Tasarımı, Tesisat Mühendisleri Derneği Teknik Yayınları: 2, Kasım I997.
2     Genceli, O.F., Ashrae Temel El Kitabi: Boru Hesapları, Tesisat Mühendisleri Derneği Teknik Yayınlar: 2, Ocak, I998.
3. lanna, W.S., I993. Introduction to Fluid Mechanics, Pws-Kent Publishing Co. Boston.
4. Shames, 1.1., 1998 Mechanics of Fluids, McGraw Hill, New York.
5. Blevins, D.R., I992. Applied fluid Dynamics Handbook, Krieger Publishing Company, Florida.
6. Schilchting, H., I979. Boundary Layer Theory, McGraw-Hill, New York.
7. Özgür, C, 1971. Deneysel Hidromekanik, İTÜ Makine Fakültesi, istanbul